Μόλις κάθισαν οι φοιτητές στις θέσεις τους, ο καθηγητής ρώτησε: “Ποιος θέλει να στοιχηματίσει μαζί μου 5 ευρώ ότι δύο άτομα σε αυτό το αμφιθέατρο, έχουν γενέθλια την ίδια ημέρα;”
Οι φοιτητές κοιτάχτηκαν μεταξύ τους. Συνυπολογίζοντας και τον καθηγητή, υπήρχαν 66 άτομα στο αμφιθέατρο. Οπότε, ενώ ο χρόνος έχει 365 ημέρες, στο αμφιθέατρο υπήρχαν μόνο 66 άτομα, Άρα οι πιθανότητες ήταν με το μέρος τους, σκέφτηκαν οι φοιτητές.
Ένα φοιτητής σήκωσε το χέρι και αποδέχτηκε το στοίχημα. Ο καθηγητής ζήτησε από όσους κάθονταν στην πίσω σειρά να αρχίσουν να φωνάζουν ένας-ένας, την ημέρα των γενεθλίων τους. Και ενώ μόλις 6 άτομα είχαν προλάβει να φωνάξουν την ημερομηνία γενεθλίων, κάποιος από την μέση του αμφιθέατρου αναφώνησε «Αυτή είναι η ημερομηνία και των δικών μου γενεθλίων”. Οπότε Ο καθηγητής κέρδισε τα 5 ευρώ.
“Θέλει κανείς άλλος να στοιχηματίσει μαζί μου;” ρώτησε.
Ένας άλλος φοιτητής σήκωσε το χέρι, υπολογίζοντας ότι οι πιθανότητες να κερδίσει είναι ακόμα μεγαλύτερες, αφού είχαν μειωθεί πια και οι πιθανότητες της τυχαίας και συμπτωματικής νίκης.
Η διαδικασία επαναλήφθηκε. Αυτή την φορά δεν μετείχε ο φοιτητής που βρέθηκε πριν να έχει ίδια ημερομηνία γενεθλίων με κάποιον άλλο. Χρειάστηκαν πάλι μόνο λίγα άτομα να φωνάξουν την ημερομηνία των γενεθλίων τους, πριν βρεθεί κάποιος άλλος φοιτητής με την ίδια ημερομηνία γενεθλίων. Ο καθηγητής κέρδισε άλλα 5 ευρώ.
«Κάποιος άλλος;” ρώτησε ο καθηγητής.
Ένας άλλος ‘γενναίος’ φοιτητής δέχτηκε το στοίχημα, αλλά και αυτός έχασε τα 5 ευρώ.
“Άλλος;”
Αυτή τη φορά οι φοιτητές ήταν διστακτικοί. Όμως μετά από λίγο σήκωσε το χέρι μου ακόμα ένας. “Τι στο καλό;” σκέφτηκε. “Για πόσο ακόμα θα είναι τυχερός ο καθηγητής;” Όμως μετά από λίγο, διαπίστωσε ότι έχασε και αυτός το στοίχημα.
Κανείς άλλος φοιτητής δεν δέχτηκε να στοιχηματίσει με τον καθηγητή …
Ο καθηγητής εξήγησε στους φοιτητές ότι αυτό το στοίχημα που έβαλε ήταν πολύ ασφαλές για τον ίδιο, παρόλο που αυτοί θεωρούσαν ότι ήταν ριψοκίνδυνο. Οι φοιτητές είχαν εκτιμήσει πολύ λάθος τις πιθανότητες επιτυχίας και αποτυχίας.
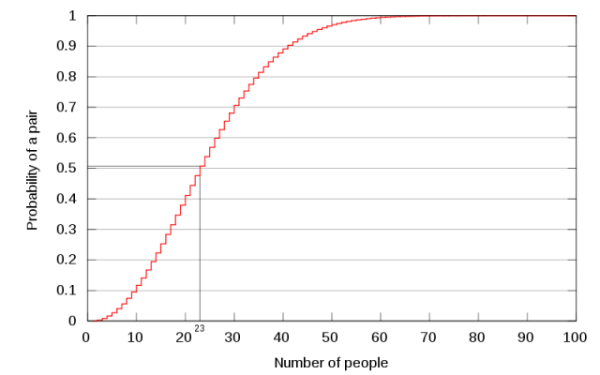
Στην πραγματικότητα, οι πιθανότητες του καθηγητή να κερδίσει το στοίχημα ήταν πάνω από 99% (!). Οι πιθανότητες θα παρέμειναν συντριπτικά υπέρ του μέχρι τα συνολικά άτομα να μειωθούν σε 23. Σε αυτό το σημείο οι πιθανότητες θα ήταν 50/50. Αυτό φαίνεται και στο παρακάτω γράφημα που δείχνει την πιθανότητα ανάλογα με τον αριθμό των ατόμων.
Το μάθημα που πρέπει να πάρουμε από την παραπάνω ιστορία είναι το εξής:
Η εκτίμηση των πιθανοτήτων δεν πρέπει να γίνεται με βάση την διαίσθηση. Αν χρειαστεί να πάρετε μια σημαντική απόφαση που απαιτεί εκτίμηση ρίσκου, μην ακούσετε το ένστικτο σας. Πολλές φορές θα αποδειχτεί λάθος (και κάποιες φορές πολύ λάθος). Αναλύστε τα δεδομένα, μελετήστε τα νούμερα, συμβουλευτείτε έναν ειδικό – αν χρειάζεται.
___
Πως υπολογίζουμε την πιθανότητα
Άν η πιθανότητα εύρεσης δύο ατόμων που έχουν την ίδια μέρα γενέθλια σε μια ομάδα 23 ατόμων είναι P(A) είναι πιο εύκολο να υπολογίσουμε την αντίστροφη πιθανότητα P(A‘) να μην υπάρχουν, δηλαδή, δύο άτομα που να έχουν την ίδια μέρα γενέθλια. Καθώς ειναι αντίστροφες ισχύει P(A‘) = 1 − P(A).
Όταν δύο γεγονότα είναι ανεξάρτητα το ένα από το άλλο τότε η πιθανότητα να ισχύουν είναι το γινόμενων των διαφορετικών πιθανοτήτων. Επομένως η πιθανότητα P(A‘) για 23 άτομα είναι P(1) × P(2) × P(3) × … × P(23).
Για ένα άτομο η πιθανότητα είναι 365/365=1 δηλαδή 100%. Για το δεύτερο άτομο η πιθανότητα να μην έχει ίδια ημέρα γενέθλια με το πρώτο είναι 364/365. Για το τρίτο άτομο είναι 363/365.
Συνεχίζοντας την ανάλυση βρίσκουμε ότι:
- P(A‘) = 365/365 × 364/365 × 363/365 × 362/365 × … × 343/365
από αυτό συνεπάγεται ότι:
- P(A‘) = 0.49270276
επομένως:
- P(A) = 1 − 0.49270276 = 0.507297 (50.7297%)
Γενικά για ν αριθμό ατόμων έχουμε:
| ν (αριθμός ατόμων) | p(ν) – πιθανότητα |
|---|---|
| 10 | 11.7% |
| 20 | 41.1% |
| 23 | 50.7% |
| 30 | 70.6% |
| 50 | 97.0% |
| 57 | 99.0% |
| 100 | 99.99997% |
____
by Αντικλείδι , https://antikleidi.com
Συναφές:
Το παράδοξο του Αχιλλέα και της χελώνας
Το λογικό παράδοξο του Επιμενίδη
Το παράδοξο με τα καλικατζαράκια
“Τα πάντα εξισορροπούνται” ή “Η τύχη δεν έχει μνήμη”
Ο Σέξτος Εμπειρικός και η ατέρμονη παλινδρόμηση της δικαιολόγησης




Ωραίο άρθρο αγαπητοί φίλοι, αλλά ας μην ξεχνάμε ότι τις μεγαλύτερες καταστροφές τις έφεραν οι υπολογισμοί και όχι οι διαισθήσεις (βλέπε οικονομικές κρίσεις)
Νομίζω ότι δεν φταίνε τα νούμερα, αλλά ο τρόπος που χρησιμοποιήθηκαν τα νούμερα.
Η στατιστική μπορεί να εφαρμοστεί με τέτοιο τρόπο ώστε να λέει την μισή αλήθεια. Είτε εσκεμμένα, είτε από μη σχετικούς με το αντικείμενο.
Mα ποιος σας ειπε οτι οι οικονομικές κρίσεις δεν ήταν προσχεδιασμένες και προβλέψιμες ?
Οι υπολογισμοί έδειχναν τι μέλλει γενέσθαι, ήξεραν και ξέρουν όλοι οτι το Ελληνικό χρέως θα φούντωνε.
Και μην ξεχνάμε το τροπάριο των τραπεζών-ιτων: ΧΡΕΟΣ=ΧΡΗΜΑ
[…] […]
[…] […]